Kunci Jawaban Soal Eksponen dan Bentuk Akar, Materi Belajar dari Rumah di TVRI Untuk Siswa SMA/SMK

BANGKAPOS.COM - Siswa SMA/SMK hari ini Selasa 28 April 2020 akan membahas soal Eksponen dan Bentuk Akar.

Meski cukup sulit, kami mencoba menyampaikan kunci jawaban dengan cukup sederhana agar adik-adik lebih mudah memahaminya.

Daftar Pertanyaan

1. Jawab pertanyaan di bawah ini :

1. a. (4)3/2 + (27)2/3 - (625)4 = ….

b. (8a2)5 (2a)3
(-4a3)4 = …..

2. Seorang peneliti bidang mikrobiologi di sebuah lembaga penelitian sedang mengamati perkembangan 50 bakteri di sebuah laboratorium.

Pada kultur bakteri tersebut, satu bakteri membelah menjadi 2 bakteri setiap jam. Akan ada berapa banyak bakteri dalam waktu 8 jam?

Jawaban :

Berikut Tribunnewswiki.com sajikan soal pertanyaan dari materi pelajaran Belajar dari Rumah di TVRI Selasa (28/4/2020), dikutip dari Hapecina.com :

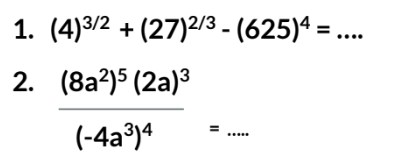
Jawaban :

1. a. Untuk soal nomor 1 kemungkinan salah ketik, seharusnya (625) pangkat 1/4 bukan pangkat 4.

Jadi hasil dari penjumlahan tersebut adalah 12

Cara dan penjelasan bisa dilihat pada gambar di bawah ini :

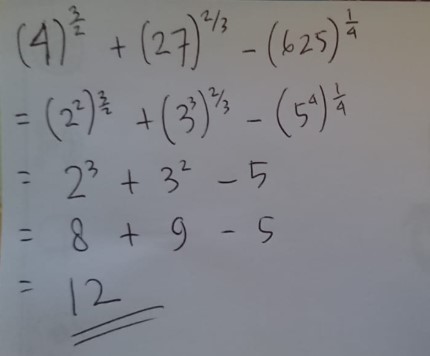
b. Jawabannya adalah 1024a

Cara dan penjelasan bisa dilihat pada gambar di bawah ini :

2. Jawaban soal nomor 2

Diketahui :

Ada 50 bakteri

satu bakteri membelah menjadi 2 bakteri setiap 1 jam

Ditanyakan : Ada berapa banyak bakteri dalam waktu 8 jam?

Jawab : 50 bakteri x 28 = 12800 bakteri

Jadi jumlah bakteri dalam waktu 8 jam adalah 12.800 bakteri.

Eksponen

 Eksponen adalah suatu bentuk bilangan perkalian dengan bilangan yang sama, kemudian diulang kembali atau pengertian singkatnya adalah suatu perkalian yang diulang-ulang.

Bilangan pada eksponen biasanya digunakan dengan lebih luas di berbagai bidang yang ada.

Seperti bidang ekonomi, biologi, kimia, fisika, dan ilmu komputer dengan aplikasi seperti perbungaan, pertumbuhan jumlah penduduk, kinetika kimia, perilaku – perilaku gelombang dan kriptografi kunci publik.

Atau ilmu yang mempelajari tentang bagaimana pesan atau dokumen seseorang aman, dan tidak dibaca oleh orang lain yang tidak berhak membacanya. 

Pemanfaatan

Bentuk eksponen bisa dinyatakan dalam bentuk persamaan maupun pertidaksamaan.

Hal itu berkaitan dengan jenis penggunaannya, misalnya untuk menyelesaikan masalah yang berkaitan dengan fungsi eksponen.

Nah, konsep dasar perkalian berulang-ulang inilah yang nantinya digunakan pemerintah untuk menghitung jumlah penduduk beberapa tahun ke depan.

Bilangan Eksponen biasa dipakai secara luas dalam  berbagai bidang.

Diantaranya seperti: pada bidang ekonomi, biologi, kimia, fisika, bahkan dalam bidang ilmu komputer dengan aplikasi.

Aplikasi tersebut diantaranya seperti:

perbungaan
pertumbuhan jumlah penduduk
kinetika kimia
perilaku – perilaku gelombang
kriptografi kunci publik atau ilmu yang mempelajari mengenai bagaimana supaya pesan atau dokumen seseoarang aman tidak terbaca oleh orang lain yang tidak berhak membacanya. 
 

Sifat

Berikut adalah beberapa sifat yang dapat kita ketahui di dalam memahami materi bilangan eksponen, diantaranya yaitu:

Pertama:

am.an = nm  +  n  (jika dikali maka pangkatnya harus ditambah)

Sebagai contoh:

52  .  53  =  52  +  3  =  55

Kedua:

 
am  :  an  =  am  –  n  (jika dibagi maka sebaliknya pangkatnya harus dikurang)

Sebagai contoh:

55 : 53 = 55 – 3 = 52

Ketiga:

( am )n  =  am x n  (jika di dalam kurung, maka pangkatnya harus dikalikan)

Sebagai contoh:

(52)3  =  52 x 3  =  56

Keempat:

(a  .  b)m  =  am  .  bm

Sebagai contoh:

(3 . 6)2  =  32 .  62

Kelima:

Sifat selanjutnya adalah sifat ke lima ini, di mana memiliki syarat bahwa “b” atau penyebutnya tidak boleh sama dengan nol (0).

(a/b)m = am/bm

Sebagai contoh:

(5/3)2 = 52/32

Keenam:

Dalam sifat yang ke enam ini, jika terdapat (an) di bawah itu merupakan bilangan positif, maka ketika dipindahkan ke atas akan berubah menjadi negatif.

Begitu pula sebaliknya, jika (an) di bawah itu merupakan bilangan negatif, maka ketika dipindahkan ke atas otomatis akan berubah menjadi positif.

Mari kita simak rumus dan contohnya di bawah ini:

1/an = a-n

Sebagai contoh:

1/ 46 = 4-6

Ketujuh:

Dalam sifat yang ketujuh ini, kita dapat menjumpai jika terdapat akar n dari am.

Jika pada saat kita sederhanakan, maka akar n akan menjadi penyebut serta akar m akan menjadi pembilang.

Dengan syarat n harus bernilai lebih besar sama dengan 2.

Contoh rumusnya ialah sebagai berikut:

n√am = am/n

Sebagai contoh:

4√36 = 46/4

Kedelapan:

Sifat ke delapan adalah bilangan eksponen nol seperti a = 1.

Sebagai contoh:

2 = 1

6 = 1

9 = 1

Syaratnya a tidak diperbolehkan sama dengan nol.

Ke delapan sifat eksponen di atas harus kita pahami sekligus harus kita hafalkan.

Sebab ke delapan sifat eksponen di atas merupakan kunci penting untuk kita dapat mengerjakan soal-soal eksponen dengan mudah. 

Fungsi

Fungsi eksponen merupakan suatu pemetaan bilangan real x ke bilangan ax dengan a  >  0 dan a  ≠  1.

Jika a > dan a  ≠  1, x∈R maka f:(x)  =  ax  lalu disebut sebagai fungsi eksponen.

Fungsi eksponen yakni, y = f(x) =  ax : a >  0 serta a  ≠  1 dengan memiliki beberapa sifat-sifat seperti berikut ini:

Kurva berada di atas sumbu x (definit positif).
Memotong sumbu y pada titik ( 0,1 ).
Memiliki asimtot datar y  =  0 (sumbu x). Arti asimtot merupakan garis yang tersebut sejajar dengan sumbu x.
Grafik monoton naik bagi bilangan x > 1.
Grafik monoton turun bagi bilangan 0 < x < 1. 
 

Bentuk

Di dalam bilangan eksponen ataupun bilangan pangkat tak selamanya selalu mempunyai nilai bulat positif, namun ada pula bilangan lain yang bernilai nol, negatif ataupun pecahan.

Berikut penjelasan dari masing-masing bilangan eksponen, diantaranya yaitu:

Bilangan Eksponen Nol (0)

Jika a  ≠  0 maka a = 1 atau a tidak diperkenankan sama dengan 0.

Sebagai contoh:

3 =1
7 =1
128 =1
y =1

Bilangan Eksponen Negatif

Jika m serta n adalah bilangan bulat positif maka:

a-n = 1/an

Sebagai contoh:

3-4 = 1/34 = 1/81

Bilangan Eksponen Pecahan

Rumus dari bilangan eksponen pecahan yaitu:

a1/n = n√a

Sebagai contoh:

21/2 = √2
21/3 = 3√2 (3)

Persamaan

Bentuk persamaan eksponen merupakan persamaan yang di dalamnya memuat pangkat-pangkat yang berbentuk sebagai fungsi dalam x di mana x merupakan sebagai bilangan peubah.

Rumus untuk persamaan eksponen antara lain:

af(x)  =  1
Jika af(x)  =  1  dengan  a>0  dan  a ≠0,  sehingga f (x)  =  0.

af(x)  =  ap
Jika af(x)  =  ap  dengan  a>0  dan  a≠0,  sehingga f(x)  =  p.

af(x)  =  ag(x)
Jika af(x)  =  ag(x) dengan  a>0  dan  a ≠0,  sehingga f (x)  =  g(x).

af(x) =  bf(x)
Jika af(x)  =  bf(x)  dengan  a>0  dan  a ≠1,  b>0  dan  b  ≠1,  serta  a≠b  sehingga f(x)  =  0.

A (af(x))2  +  B(af(x))  +  C  =  0
Dengan  af(x)  =  p,  maka  bentuk dari persamaan di atas bisa kita ruba ke dalam persamaan kuadrat seperti: Ap2  +  Bp  +  C  =  0. (3)

(TRIBUNNEWSWIKI.COM/PUTRADI PAMUNGKAS)

LIVE STREAMING TVRI

Link Live Streaming TVRI Belajar dari Rumah dapat diakses melalui tautan berikut :

LINK 1

LINK 2

(Tribunnewswiki.com/Ekarista/Putradi)

Artikel ini tayang di Tribunnewswiki.com berjudul Soal dan Jawaban Lengkap Materi Belajar dari Rumah di TVRI untuk SMA/SMK Selasa 28 April 2020